　見聞伝　＞　戸塚洋二の科学入門　＞　科学入門シリーズ　４

科学入門シリーズ４
１９世紀末　科学の困難　光の科学

第3回　　２．７２５Ｋのるつぼから出る電波、黒体放射

　前回、るつぼの中の光は、１９００年以前の物理理論で導いた式で説明できないことを説明しました。理論的な式の一つはレーリー・ジーンズと呼ばれる式で、るつぼの温度、光の振動数、それに光速だけで表わされました。もう一つのウィーンの式は、考え方がだいぶ違っていて、そのため式の形も大きく異なります。最も大きな違いは、新しい普遍的な定数ｈが入ってきて、光のエネルギーはその振動数をｆとして「ｈｆ」と表わされることでした。この考えは、ウィーンの変位則という観測事実を使って導いたものです。だからウィーンの式は当時の理論に一部新たな観測事実を付け加えて改良したものと考えることができます。ｈという新しい定数を使っているのもそのためです。

　後知恵ですが、ウィルヘルム・ウィーンは、なぜ、光のエネルギーが振動数に比例するということを深く考えなかったのでしょうか。Ｅ＝ｈｆという式は、当時の理論では全く理解できなかったのですから。１９００年にウィーンはまだ３６歳の若さでしたが、当時の考えから抜け出せなかったことを示しています。科学のブレークスルーを導くのがいかに難しいかがわかると思います。

　それでは、温度をマイナス２７０℃（絶対温度２．７２５Ｋ）で両方の式がどうなるかを示したいと思います。

　絶対温度が２．７２５Ｋでは、るつぼの中のマイクロウエーブの振動数は１００～５００ギガヘルツくらいに広がっています。下のグラフが両方の式をマイクロウエーブの振動数を横軸にとって表しました。黄色がレーリー・ジーンズの式、赤がウィーンの式です。観測値は、「プランクの式」と書かれている曲線でよく表わされます。つまり、ウィーンの式は振動数の高いスペクトルをうまく説明しますが、振動数の低いところでは観測値からずれてきます。レーリー・ジーンズの式は、振動数のずっと小さなところで観測値とやっと一致し、振動数がちょっと高くなると全然合いません。

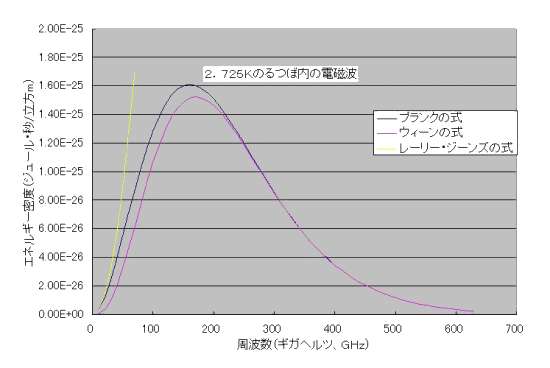
　プランクの式は後で説明します。

　このようにるつぼの中の電波（光）のふるまいは、当時の理解を超えていたのです。るつぼの中というと何か現実世界とはあまり関係ない現象のような気がします。鉄を溶かす溶鉱炉の中はるつぼに近いのです。当時の作業者は、溶鉱炉の温度を上げると、小窓から見える内部は光で満たされ、温度が上がると光の色は赤から白色に移ることは知っていました。つまり、あふれた現象だったのですが、人々はあまり深く考えなかったのです。

　その後、るつぼ内の光の振動数分布（スペクトル分布）は、光を完全に吸収する物体が熱せられた時に発する光のスペクトル分布と全く同じである、ということもわかりました。そこで今まで説明してきた光のスペクトル分布を「黒体放射」といいます。この放射の光の強さは黒体やるつぼを作っている材料に依らず、普遍的な定数と振動数、絶対温度だけで表わされるはずです。ダルマストーブ、太陽や星は、黒体放射に近いスペクトルで光を発しています。

　ところで、私がなぜ２．７２５Ｋという極低温を選んだのか次回に説明しましょう。　　（続く）

←　前の記事へ

→　次の記事へ
→　表紙へ戻る