| 丂尒暦揱丂亜丂屗捤梞擇偺壢妛擖栧丂亜丂壢妛擖栧僔儕乕僘丂係 |
 |
丂崱擔偐傜壢妛擖栧僔儕乕僘戞係抏傪巒傔傑偡丅傑偨棟孅偭傐偄榖偵側傝傑偡偑丄変枬偟偰偔偩偝偄丅巹偺峫偊傕擖偭偰偄傞偺偱丄揱摑揑側愢柧偲偼偪傚偭偲堘偭偰偄傑偡丅偙偺曽偑巹偵偼棟夝偟傗偡偐偭偨偺偱偡丅
壢妛擖栧僔儕乕僘係
侾俋悽婭枛丂壢妛偺崲擄丂岝偺壢妛
戞1夞丂丂岝偺壢妛偲懢梲偺僄僱儖僊乕尮
丂俀侽悽婭偼暔棟妛偺悽婭偲屇偽傟傞戝曄側壢妛媄弍偺恑曕偑偁傝傑偟偨丅傑偝偵搟摀偺傛偆側惃偄偱偟偨丅偦偺婎慴偲側偭偨偺偼丄検巕椡妛偲乮摿庩乯憡懳惈棟榑偱偡丅偙偺傛偆側忢幆傪暍偡傛偆側怴偟偄朄懃偼丄悢妛偺傛偆偵恖偺摢擼偺拞偱嶌傜傟偨傕偺偱偼偁傝傑偣傫丅侾俋悽婭枛丄恎嬤偵偁傞尰徾傪傛偔娤嶡偟偰傒傞偲丄崱傑偱偺峫偊偱偼偳偆偟偰傕愢柧偱偒側偄尰徾偑尒偮偐偭偨偺偱偡丅壢妛幰偼丄偦傟傜偺娤應帠幚傪側傫偲偐乮悢妛揑偵乯愢柧偟傛偆偲戝曄側嬯楯傪廳偹丄偮偄偵怴偟偄朄懃傪敪尒偟傑偟偨丅偙偺恎嬤偵偁偭偰摉帪棟夝偱偒側偐偭偨尰徾傪愢柧偟偨偄偲巚偄傑偡丅
丂棟夝偱偒側偐偭偨尰徾偺堦偮偼丄懢梲偺僄僱儖僊乕尮偱偡丅偙偺偍榖偼偡偱偵僔儕乕僘俀丒戞1夞偱徯夘偟傑偟偨丅妀梈崌斀墳偑偦偺撲傪夝偔僇僊偩偭偨偺偱偡偑丄偦偺婎慴偲側偭偨偺偼傾僀儞僔儏僞僀儞偺乮摿庩乯憡懳惈棟榑偱偟偨丅憡懳惈棟榑傕丄偄偢傟屻偺擖栧曇偱傢偐傝傗偡偔愢柧偟傑偡丅
丂崱夞偼偦傟埲奜偺尰徾偺堦偮傪徯夘偟傑偟傚偆丅偙傟偼乽岝乿偵娭偡傞尰徾偱偡丅岝偼偛懚偠偺傛偆偵侾昩娫偵抧媴傪俈夞傝敿丄俁侽枩倠倣憱傝傑偡丅偙偺懍搙偑僇僊偱偡丅晛捠偺暔懱偼偢偭偲抶偄懍搙偱偟偐摦偔偙偲偑偱偒傑偣傫丅偦偺抶偄悽奅偱偼丄暔懱偺摦偒偼僯儏乕僩儞偵傛偭偰懪偪棫偰傜傟偨朄懃偵傛偭偰偆傑偔愢柧偡傞偙偲偑偱偒傑偡丅岝偼揹帴攇偺堦庬偱偡偑丄偦偺婎杮偲側傞朄懃丄儅僋僗僂僄儖偺朄懃丄偼侾俋悽婭敿偽偵妋棫偝傟傑偟偨丅偦偺朄懃偺拞偱丄岝懍乮們偲彂偔乯偼揹帴攇傪昞偡傕偭偲傕婎杮揑側掕悢偩偲偄偆偙偲偑傢偐傝傑偟偨丅
丂岝偺娤應丄摿偵岝偺攇挿傗怳摦悢偺應掕媄弍偑媫懍偵敪払偟丄懢梲岝偑偳偺傛偆側攇挿偺岝偱惉傝棫偭偰偄傞偐丄偮傑傝丄懢梲岝偑丄偳偺傛偆側怓偺岝偑崿偠偭偨傕偺側偺偐側偳丄偄傢備傞乽僗儁僋僩儖娤應乿偑崅偄惛搙偱偱偒傞傛偆偵側傝傑偟偨丅
丂梟峼楩傗摡帴婍傪嶌傞梣傪偺偧偒憢偐傜尒傞偲丄撪晹偺壏搙偲偲傕偵丄拞偺岝偺怓偑愒偐傜敀怓偵曄傢偭偰偄偔偺偑娤嶡偝傟傑偡丅傑偨丄愇桘傗恉傪擱傗偡僟儖儅僗僩乕僽偺奜懁偑丄壏搙偑忋偑傞偵偮傟偰愒偔岝偭偰偔傞偙偲傕摨偠尰徾偲峫偊傜傟偰偄傑偡丅
丂梟峼楩偼栵夘偱偡偐傜丄懴壩惈偺揝傗悾屗暔側偳偱偱偒偨毊毮乮傞偮傏乯傪梡堄偟傑偡丅傞偮傏偺岥偼彫偝偔丄拞偑傗偭偲尒偊傞偔傜偄偵偟傑偡丅拞偵壗傕擖傟側偄偱丄傞偮傏傪壛擬偟偰偄偒傑偡丅壛擬偟偰偄傞娫丄傞偮傏偺岥偐傜側偐傪擿偄偰傒傞偙偲偵偟傑偟傚偆丅壏搙偑掅偄帪偼拞偼埫偔偰壗傕尒偊傑偣傫丅壏搙偑悢侾侽侽搙偵側傞偲丄撪晹偼愒偔岝傝巒傔傑偡丅偮傑傝愒擬偟傑偡丅偝傜偵壏搙傪忋偘偰偄偔偲丄撪晹偺怓偼愒偐傜墿怓傊丄偝傜偵敀偔岝傝婸偒傑偡丅敀擬忬懺偱偡偹丅丂
丂抧忋偱偼偙傟埲忋壏搙傪忋偘傞偙偲偼偱偒傑偣傫丅塅拡偺偍惎偝傑偼壗傜偐偺曽朄偱惎慡懱偑擬偣傜傟偰偄偰丄偦偺忬懺偼偪傚偆偳傞偮傏偺撪晹偺忬懺偵側偭偰偄傞偲峫偊傜傟傑偡丅僟儖儅僗僩乕僽偺奜懁偑岝傞偺偲摨偠尨棟偱偡丅偦偙偱偄傠偄傠側惎傪娤嶡偟偰傒傞偲丄敀擬偐傜偝傜偵惵偔丄偦偟偰偮偄偵偼巼奜偱岝傝婸偄偰偄傞惎傪敪尒偡傞偙偲偑偱偒傑偡丅
丂偮傑傝丄傞偮傏傪壛擬偡傞偲丄偦偺撪晹偼岝偱枮偨偝傟丄壏搙偲偲傕偵怓偑愒偐傜墿怓丄敀傊丄偝傜偵惵偐傜巼奜慄偵傑偱曄傢偭偰偄偒傑偡丅傞偮傏偺憢偐傜尒偊傞岝偺僗儁僋僩儖暘晍丄偡側傢偪怳摦悢暘晍傪應偭偰傒傑偡丅偦偺寢壥師偺偙偲偑傢偐傝傑偟偨丅
嘆傞偮傏撪晹偺怓偼偄傠偄傠側怳摦悢偺岝偑崿偠傝崌偭偰偱偒偰偄傞偑丄堦斣嫮偄岝偺怳摦悢偵拲栚偡傞偲丄偦偺怳摦悢偼傞偮傏撪晹偺愨懳壏搙偵斾椺偡傞丅乽僂僀乕儞偺曄埵懃乿
嘇岝偺怳摦悢暘晍偼傞偮傏偺暻偺嵽幙偵娭學側偔丄忢偵摨偠宍傪偟偰偄傞丅
嘊岝偺怳摦悢暘晍偼丄偁傞怳摦悢偱岝偺嫮偝偑嵟傕戝偒偔側傝丄怳摦悢偑偦偺抣偐傜崅偄曽傗掅偄曽偵偢傟偰傕岝偺嫮偝偼庛傑偭偰偄偔丅
丂埲忋偑娤應偱暘偐偭偨偙偲偺堦晹偱偡丅怳摦悢暘晍傪嶲峫偺偨傔偵壓偵帵偟傑偡丅
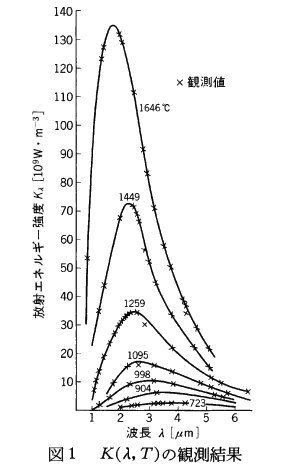
暔棟妛帿揟丒嶰掶斉乮攟晽娰乯丄俀侾俋俀儁乕僕傛傝堷梡
丂摉帪偺壢妛偱偼嘆傕嘊傕愢柧偡傞偙偲偑偱偒側偄丄偲偄偆偙偲偑傢偐偭偨偺偱偡丅
丂愨懳壏搙乮愛巵壏搙亄俀俈俁亷丄扨埵偼俲乯偲偄偆偺偼暘巕偺擬塣摦偵娭學偟偰偄傑偡丅壏搙偼暘巕侾屄丄惓妋偵尵偆偲暘巕偺忬懺乮帺桼搙偲偄偆乯侾偮偁偨傝偺僄僱儖僊乕偩偲偄偆偙偲偼暘偐偭偰偄傑偟偨丅偩偐傜丄壏搙偼僄僱儖僊乕偵曄姺偱偒偰丄愨懳壏搙傪俿丄暘巕偺僄僱儖僊乕傪俤偲偡傞偲丄斾椺掕悢傪倠偲偟偰娙扨偵丄
丂丂丂丂丂丂丂丂丂丂俤亖倠俿
偲彂偔偙偲偑偱偒傑偡丅
丂岝偺怳摦悢傪倖偲偟偰傒傑偟傚偆丅娤應帠幚嘆偼丄偁傞掕悢倛傪帩偭偰偒偰丄
丂丂丂丂丂丂丂丂丂丂丂丂倛倖/倠俿亖堦掕偺悢抣
偩丄偲偄偆傆偆偵昞偣傑偡丅乮乽/乿偼妱傝嶼傪昞偟傑偡丅乯堦掕偺悢抣偲偄偆偺偼丄偦傟偼扨側傞悢偱偁偭偰丄懍搙側偳偺傛偆偵扨埵傪帩偭偨娤應検偱偼側偄丄偲偄偆偙偲傪昞偟傑偡丅乮偙偺愢柧偼傕偭偲傕傜偟偄偱偡偹丅惓妋偵尵偆偲傕偆彮偟徻偟偄媍榑偑昁梫偱偡丅偦偺僸儞僩偼僂傿乕儞偺僲乕儀儖徿島墘偵偁傝傑偡丅偪傚偭偲擄偟偄偱偡偑丅乯
丂幚偼偙偺幃偑摉帪偺棟榑偱愢柧偱偒側偐偭偨偺偱偡丅崱偐傜峫偊傟偽棟桼偼娙扨偱偡丅揹帴攇丄堦斒偵攇偺僄僱儖僊乕偼丄怳摦悢偵埶傜偢偵偦偺怳暆偺俀忔偵斾椺偡傞丄偲偄偆偺偑摉帪偺棟榑偑庡挘偡傞偲偙傠偱偡丅幚嵺丄壒攇傗僶僀僆儕儞側偳偺尫偺怳摦偱偼偦偺傛偆偵側偭偰偄傑偡丅儅僋僗僂僄儖偺揹帴攇棟榑傕椺奜偱偼偁傝傑偣傫丅
丂偲偙傠偑丄忋偺幃偺堄枴偡傞偲偙傠偼偙偆偱偡丅倠俿偼僄僱儖僊乕傪昞偡偺偱偡偐傜丄幃傪偪傚偭偲曄宍偟偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂倛倖亖乮堦掕偺悢抣乯丒乮倠俿乯
偱偡偐傜丄倛倖偑岝偺僄僱儖僊乕傪昞偡偼偢偱偡丅乮乽丒乿偼妡偗嶼傪昞偟傑偡丅乯倖偼怳摦悢偱怳暆偱偼偁傝傑偣傫丅偙傟偼柕弬偱偡丅
丂巹偨偪偑暔帠傪昞偡帪丄幙検丄挿偝丄帪娫偺俁偮偑傢偐傟偽廫暘偱偡丅摉帪丄婎杮揑側掕悢偱丄偙偺俁偮偺扨埵偱昞偣傞傕偺偼丄僯儏乕僩儞偺枩桳堷椡偲岝懍偩偗偱偟偨丅忋偺倠傕婎杮掕悢偩傠偆偲偄偆惡偑暦偙偊傞偐傕偟傟傑偣傫丅妋偐偵偦偆偱偡偑丄倠偼幙検丄嫍棧丄帪娫偱昞傢偡偙偲偼偱偒偢丄恖娫偑彑庤偵寛傔偨乽搙乿偲偄偆傛偆側扨埵偑擖偭偰偔傞偺偱偩傔偱偡丅
丂怳摦悢偼丄侾昩偁偨傝攇偑壗夞怳摦偡傞偐傪昞偟偰偄傑偡偐傜丄偦偺扨埵偼
乽侾/帪娫乿
偲側傝傑偡丅夞悢偼扨偵悢偱偡偺偱扨埵偲偼尵偄傑偣傫丅僄僱儖僊乕偺扨埵偼
乽幙検丒乮嫍棧偺俀忔乯/乮帪娫偺俀忔乯乿
偱偡丅偩偐傜丄忋偺掕悢倛偼
丂丂丂丂丂丂丂丂乽僄僱儖僊乕丒帪娫乿
偡側傢偪
丂丂丂丂丂丂丂丂乽幙検丒乮嫍棧偺俀忔乯/乮帪娫乯乿
偺扨埵傪帩偪丄岝懍傗枩桳堷椡掕悢偲摨偠婎杮揑側掕悢偲峫偊傞偙偲偑偱偒傑偡丅
丂僯儏乕僩儞偺椡妛傗儅僋僗僂僄儖偺揹帴棟榑偑偦傟偧傟枩桳堷椡掕悢傗岝懍傪婎杮偲偟偰偱偒偰偄傞傛偆偵丄偙偺怴偟偄扨埵傪帩偭偨掕悢偺摫擖偼丄偙偺掕悢傪婎杮偵帩偮丄傑偭偨偔怴偟偄棟榑傪昁梫偲偟偰偄傞偺偱偡丅
丂倠俿偼侾偮偺暘巕偺塣摦傪昞偡僄僱儖僊乕偱偟偨丅倛倖偼岝偺僄僱儖僊乕偱偡偑丄岝偼攇偱偡偐傜丄嬻娫偵峀偑偭偰恑傒傑偡丅暘巕偺傛偆偵僣僽僣僽偵暘妱偱偒側偄偼偢偱偡丅偱偼丄暘巕偵懳墳偡傞岝偺僄僱儖僊乕倛倖偼偳傫側堄枴偑偁傞偺偱偟傚偆丅偙傟傕夝寛偟側偗傟偽側傜側偄媈栤偱偡丅丂丂丂丂乮懕偔乯
|
|
| Copyright (C) 2008 屗捤梞擇,丂搶嫗戝妛 棫壴棽僛儈僫乕儖丂All Rights Reserved.丂丂昞帵偑曵傟傑偡偐丠丂 |
|